Coherence Retrieval (Phase Space Tomography)

By capturing the amplitude and phase profile at the cross section of a coherent light beam, we can predict its behavior at a macroscopic time scale when traversing known optical systems. Such is the basis for holography, where a coherent field can be recorded, and then reconstructed physically or propagated digitally. However, most light we encounter everyday is not coherent, but rather partially coherent, and hence simply the amplitude and phase is not enough to capture the information contained in such beams; in fact, phase has no defined value in a partially coherent beam as it is stochastically varying. What is sufficient is a recording of the two-point correlation of the field—for the polychromatic case, this information is contained in the mutual coherence function or cross spectral density, and for the quasimonochromatic case, this information is given by the mutual intensity or phase space representations such as the Wigner distribution or the ambiguity function.

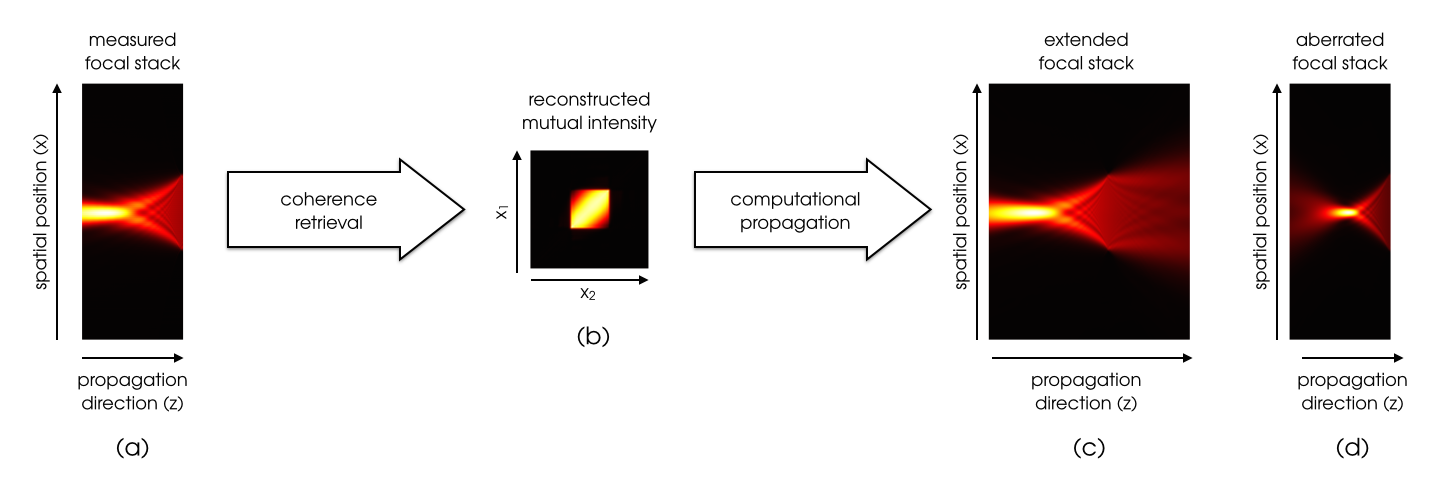
Illustration of coherence retrieval
Coherence retrieval can be used to compute the mutual intensity (b) of a partially coherent beam from a measured focal stack (a). Once computed, the mutual intensity can then be computationally propagated through arbitrary optical systems to generate for example an extended focal stack (c) or a focal stack of the same beam propagated through an aberrated system (d).

Although we are interested in a correlation function, the standard signal processing method of estimating correlation using measurements of many realizations is not feasible for most optical applications, because the oscillations of the electromagnetic field are much too fast for any currently available apparatus to capture directly. What can be measured is time-averaged intensity of the field in question, perhaps after it has propagated through some linear optical system(s) of our own choosing. We can then estimate the correlation function by solving an inverse problem based on these measurements, in a process called coherence retrieval or phase space tomography. The latter term derives from the fact that intensity cross-sections of a partially coherent beam correspond to projections of the Wigner distribution or slices of the ambiguity function, and thus focal stacks or apparatuses with cylindrical lenses have been the focus of most of the physics literature. In the geometric optics limit, phase space tomography becomes light field imaging, which has recently spawned many sensing and illumination applications in the computer graphics literature.

(primal form)
$ \begin{aligned} \underset{\vec{J}}{\arg\min}& \sum_{m=1}^M \sigma_m^{-2}\left(y_m - \vec{k}^{\mathsf H}_m \vec{J} \vec{k}_m\right)^2 \\ \text{subject to } &\vec{J} \succeq \vec{0} \end{aligned} \quad $
(factored form)
$ \quad \begin{aligned} &\underset{\vec{X}}{\arg\min} \sum_{m=1}^M \sigma_m^{-2}\left(y_m - \vec{k}^{\mathsf H}_m \vec{X}\vec{X}^{\mathsf H} \vec{k}_m\right)^2 \end{aligned} $
The primal form above is an inverse problem which asks for the mutual intensity $\vec J$ that, when propagated through known optical systems described by the $\vec k_m$ vectors, results in the smallest weighted error compared to the $M$ measured intensities given by the $y_m$s, assuming noise standard deviations specified by the $\sigma_m$s. One way to solve this constrained problem is to perform a factorization step, yielding a quartic function in $\vec X$, which is a generalized coherence modes decomposition of the mutual intensity.

We have formulated coherence retrieval as a constrained least squares problem that ensured results were physically valid while assuming weighted Gaussian measurement noise. The formulation can be applied to any measurement system as long as the system impulse response is known and measurement noise can be adequately modeled as Gaussian. A factorization approach was used to convert the formulation into an unconstrained problem, which could be solved using a nonlinear conjugate gradients algorithm called factored form descent. We have used this approach to initially solve for the mutual intensity of a 1D Schell-model source, and current work includes adding regularizers and preconditioners to improve convergence, investigating new capture protocols to exploit the versatility of the formulation, and using recent state-of-the-art convex optimization approaches to solve this inverse problem.

Relevant Articles and Conference Proceedings